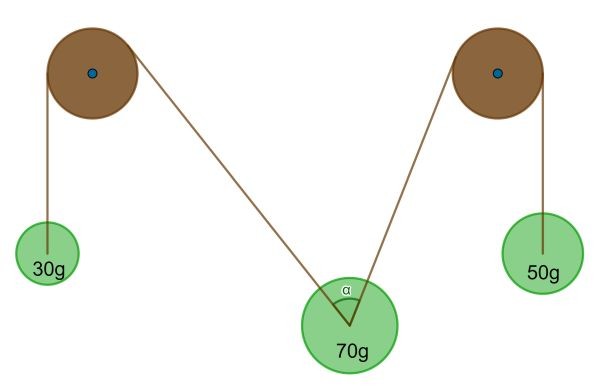
De vraag van deze week gaat over twee katrollen en drie gewichten die in een statisch evenwicht zijn. De gewichten zijn 30, 50 en 70 gram, waarbij het zwaarste in het midden hangt.
De vraag is nu: gegeven deze evenwichtstoestand, wat is dan de hoek α van de knik in het ophangtouw? Je mag het gewicht van het touw alsmede de wrijving verwaarlozen.
Vectoren zijn het antwoord
Om het antwoord op de vraag te vinden moet je bedenken dat de zwaartekracht op de drie gewichten aanleiding geeft tot drie vectoren in het ophangpunt van de middelste. Eén verticaal naar beneden van dat gewicht zelf en twee langs het touw gericht van de buitenste gewichten. Die zijn in evenwicht, hetgeen betekent dat de eerste vector precies tegengesteld is aan de som van de laatste twee. Ik heb dat hier geschetst:
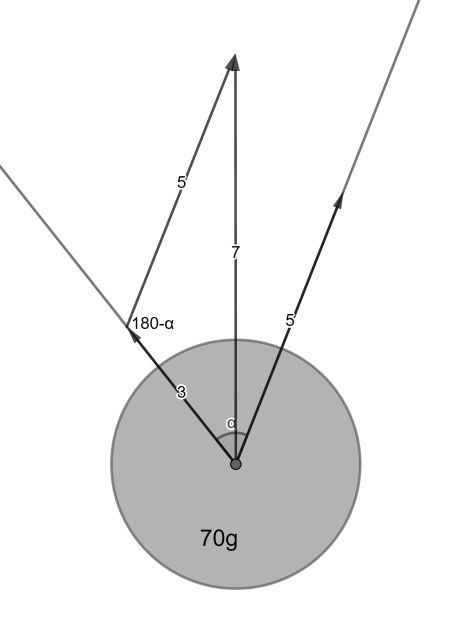
Om het simpel te houden heb ik ze even geschaald naar lengte 3, 5 en 7. Nu zie je een driehoek verschijnen met als hoek 180-α. Je kunt nu de cosinusregel toepassen: 9+25-30cos(180-α)=49. Dit kun je reduceren tot cos(α)=1/2 en dus α=60°.
Een mechanische hoekgenerator
Het is toch opzienbarend dat je met zo’n simpele opstelling een hoek van 60° kunt produceren? En je kunt natuurlijk elke andere hoek krijgen kleiner dan 180° door de gewichtjes te variëren. Ziehier een simulatie van de mechanische hoekgenerator.
En als je wilt zien hoe je met gewichten in de verhouding 3 : 4 : 5 een rechte hoek produceert, kijk dan deze video.