Je hebt twee munten met de straalverhouding 1 : 2. Je rolt de kleine munt precies éénmaal om de omtrek van de grote zonder te slippen. Hoeveel keer is de kleine munt dan om zijn as gedraaid?
Het foute antwoord
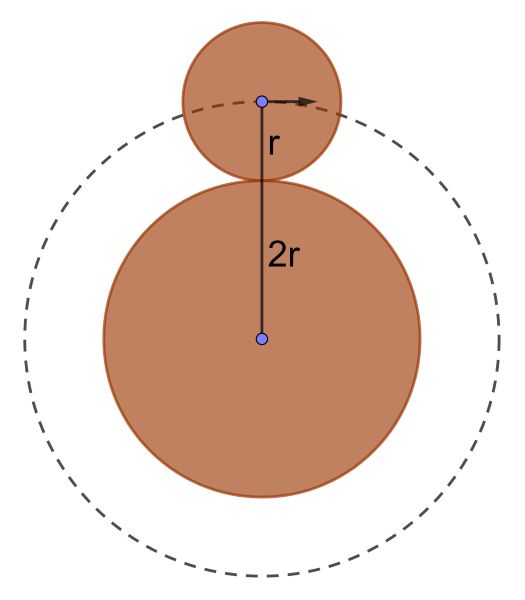
Je kunt als volgt redeneren: de omtrek van de kleine munt (2πr) is precies de helft van die van de grote munt (4πr). Hij rolt dus twee keer om de volledige omtrek van de grote munt te halen. Twee omwentelingen dus?
Fout, deze redenering zou kloppen als de 4πr op een rechte lijn zou liggen. Echter, de grote muntomtrek is geen rechte lijn, maar een gekromde en tevens gesloten lijn.
Het goede antwoord
Het goede antwoord neemt, naast de bovengenoemde rotatie, ook de revolutie mee van het gehele referentiesysteem van de kleine munt. Je moet er dus 1 bij optellen. Hij zal dus niet twee- maar driemaal om zijn as draaien, zoals ook te zien is in onderstaande animatie.
Gelijke munten
Wat nu als de munten gelijk zijn? Volgens dezelfde redenering zal de rollende munt dan tweemaal om zijn as draaien voor hij weer terug is op dezelfde plek.
Derhalve zal hij bij een halve omwenteling precies éénmaal om zijn as draaien, zoals te zien is in onderstaande video.
